Find the Unit Circle
Degrees, Radians, and π
Understanding the unit circle begins with knowing how degrees, radians, and π connect. When measuring angles, we often use degrees: for example, a straight line is 180 degrees, and a full circle is 360 degrees. But radians offer a unique way to measure angles, directly linking them to the circle’s geometry using π. In this method, π radians equals 180 degrees, and a full circle equals 2π radians.
For example, converting 270 degrees to radians involves multiplying by the conversion factor π/180, resulting in 3π/2 radians. Similarly, π/6 radians equals 30 degrees when converted. This seamless interchange between radians and degrees is vital when exploring the unit circle, where measurements are often tied to π.
Unit Circle and Trigonometry
The unit circle is a simple yet powerful tool in trigonometry. It’s a circle with a radius of one, centered at the origin of a graph. While its small size makes calculating the circumference or area straightforward, its real importance lies in how it connects angles, radians, and right triangles.
Imagine drawing a line from the circle’s center to its edge, forming an angle with the horizontal axis. By projecting this line vertically and horizontally, we create a right triangle. The triangle’s sides correspond to the sine and cosine of the angle, and these values are pivotal in solving trigonometric problems. Visualizing these relationships on the unit circle makes it easier to understand concepts like π radians, 30 degrees, and their role in mapping angles to coordinates.
Video
Understanding SOHCAHTOA: A Shortcut for Trigonometry
The term SOHCAHTOA is a simple and powerful way to remember how to calculate the trigonometric ratios of sine, cosine, and tangent. It represents the relationships between the angles and sides of a right triangle. Here’s what it stands for:
- Sine (SOH) = Opposite / Hypotenuse
- Cosine (CAH) = Adjacent / Hypotenuse
- Tangent (TOA) = Opposite / Adjacent
For example, if you’re given a right triangle where one angle is 30 degrees, and you know the hypotenuse is 10, you can use SOHCAHTOA to find the other sides. Using sine, you’d calculate the length of the opposite side as sine(30°)×hypotenuse\text{sine(30°)} \times \text{hypotenuse}sine(30°)×hypotenuse, which is 0.5×10=50.5 \times 10 = 50.5×10=5.
Applying SOHCAHTOA to Real-Life Problems
SOHCAHTOA isn’t just a classroom trick—it’s a tool used in many real-world scenarios, such as engineering, construction, and navigation. If you’re building a ramp and know its length (hypotenuse) and angle, you can use cosine to determine the horizontal distance (adjacent side) or sine to find the height (opposite side). Similarly, tangent can help in designing slopes or calculating angles for road inclines.
By remembering SOHCAHTOA, you can quickly solve complex problems involving angles and triangles, bridging the gap between theory and practical application.
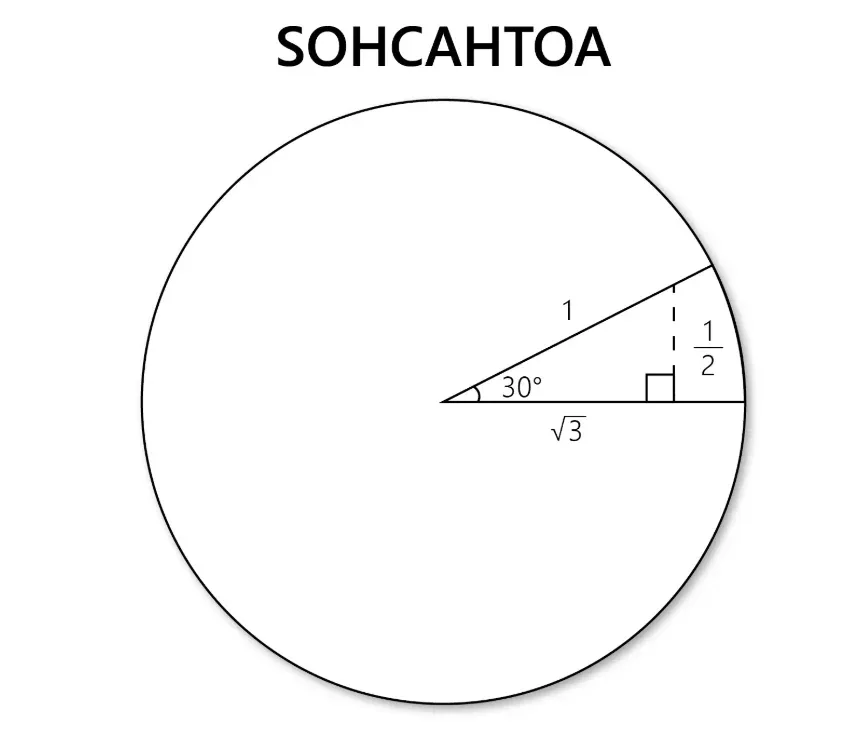
The unit circle has a radius of 1, and we can use SOHCAHTOA to find the sides of a triangle. For instance, the opposite side is 1/2, and the adjacent side is √3/2.
Think of the unit circle as a handy tool that organizes common right triangles. It helps us easily recall sine and cosine values for important angles. The spot where the line from an angle touches the circle gives us these values. For example, a line at a 60° angle intersects the circle at (1/2, √3/2). Here, the x-coordinate represents the cosine, and the y-coordinate represents the sine. To find the tangent, divide the y-coordinate by the x-coordinate. So, for 60°:
- sin(60°) = √3/2
- cos(60°) = 1/2
- tan(60°) = (√3/2) ÷ (1/2) = √3
It’s also important to make sure angles are in standard position. This means the angle starts at the center of the circle, with one side along the positive x-axis and the other side rotating counterclockwise to the correct angle. If an angle isn’t in this position, adjust it before finding your trig values.
Unit Circle Practice Questions
QuizBanga, No. 1 website for Simulation Mock tests
