Rotations

Master Rotations Instantly: Find the Perfect Angle!

Rotations are a natural part of the world around us. The earth rotates on its axis, creating the cycle of day and night. Similarly, the wheel on a car or bicycle rotates around its center bolt, completing full 360° turns. Not all rotations are complete circles; some, like those in video games, involve characters or objects rotating less than 360°. In geometry, rotation is a type of transformation where a figure turns about a point called the center of rotation, maintaining its shape and size while changing direction.

A Ferris Wheel is another example of rotation in real life. Its center hub acts as the center of rotation, allowing the wheel to turn smoothly. Rotations can be clockwise or counterclockwise, depending on the direction needed. This simple motion can be observed in many forms, whether in mechanical systems or in nature, highlighting how essential and versatile it is in our everyday experiences.

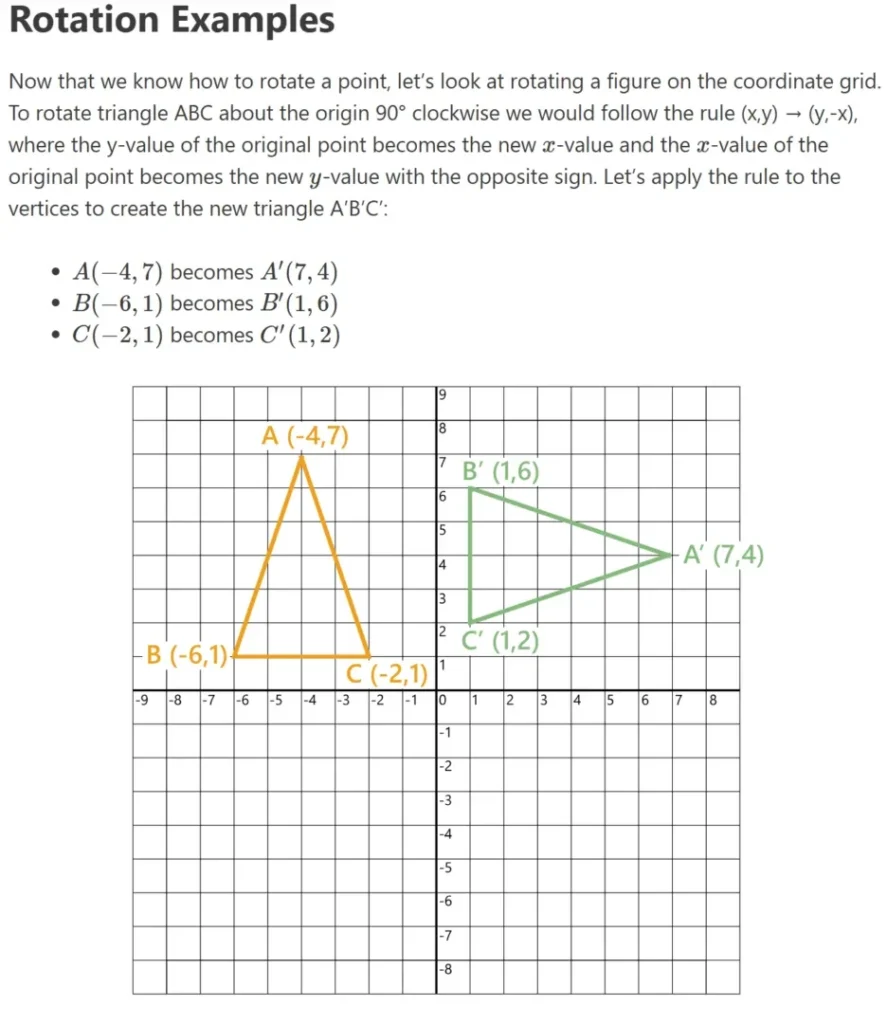
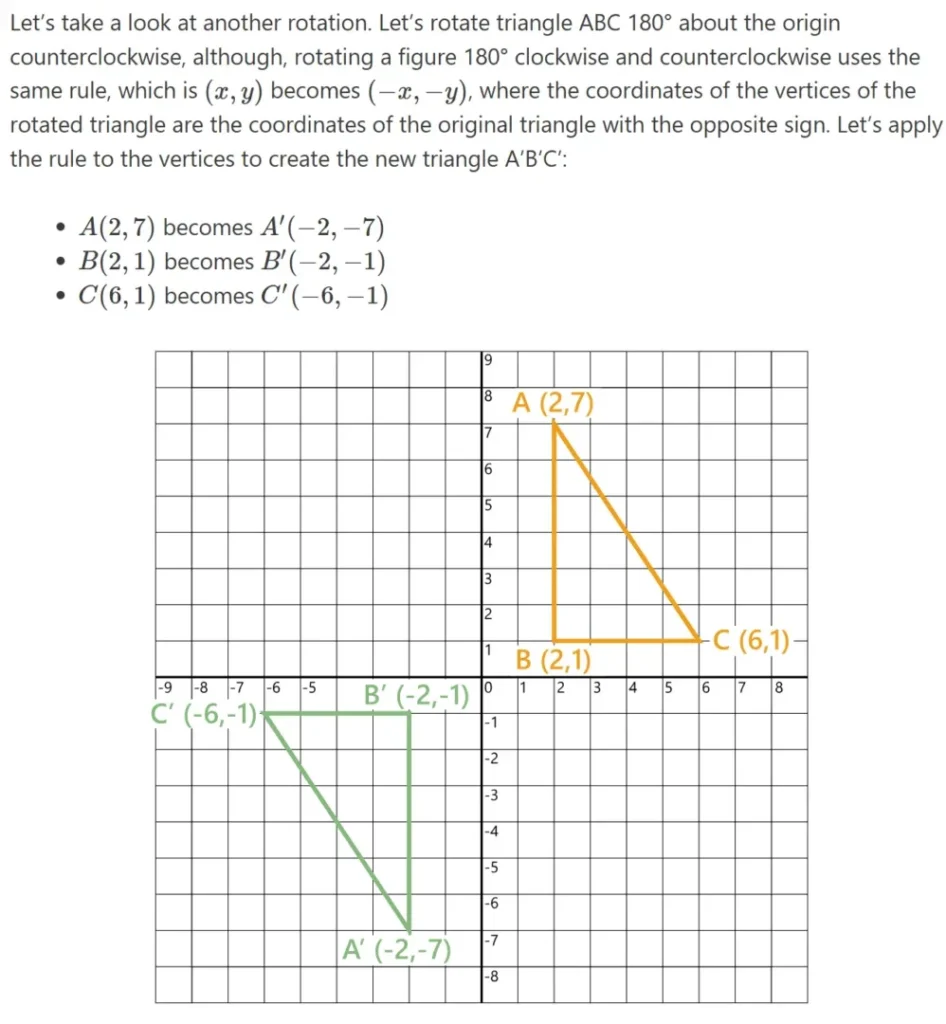
A useful tool for demonstrating rotations is the coordinate grid. Let’s explore how rotating a point around the origin (0,0) works. By plotting a point on a coordinate grid and rotating the paper 90° or 180° either clockwise or counterclockwise, we can determine the new position of the rotated point.

For example, consider point A at (5,6). Rotating the paper 90° clockwise around the origin moves point A to A′ at (6,−5). Similarly, when point A at (5,6) is rotated 180° counterclockwise around the origin, it becomes A′ at (−5,−6).

Now, let’s analyze these rotations in detail. In the first case, rotating point A(5,6) 90° clockwise results in point A′(6,−5), where the original y-value becomes the new x-value, and the original x-value becomes the new y-value with its sign reversed. In the second case, rotating point A(5,6) 180° counterclockwise results in A′(−5,−6), where both the x- and y-values retain their positions but have opposite signs.

Rotation Rules

• A 90° clockwise rotation transforms (x,y)(x, y) into (y,−x)(y, -x).
• A 90° counterclockwise rotation transforms (x,y)(x, y) into (−y,x)(-y, x).
• A 180° rotation, whether clockwise or counterclockwise,
  transforms (x,y)(x, y) into (−x,−y)(-x, -y).
• A 270° clockwise rotation transforms (x,y)(x, y) into (−y,x)(-y, x).
• A 270° counterclockwise rotation transforms (x,y)(x, y) into (y,−x)(y, -x).

Rotation Video

Rotation Practice Questions

0

Rotation

1 / 4

A water wheel has a diameter of 20 feet. Water from a water trough that is positioned above the water wheel is poured into the paddles of the water wheel to force it to rotate in a clockwise direction. The water in a paddle begins to be released from the water wheel after it makes a 90° rotation. If the water enters the paddle at the point shown on the graph in the coordinate plane below, what are the coordinates of the point where the water is released from the water wheel? The center of the water wheel is at the origin of the coordinate plane.

(−9,−3)

(9,−3)

(−3,−9)

Rotating a point that has the coordinates (x,y)(x,y) 90° about the origin in a clockwise direction produces a point that has the coordinates (y,−x)(y,−x). Substituting the coordinates for the point where the water enters a paddle into our formula, we get our rotated point of (9,−3)(9,−3). Thus, the coordinates of the point where the water is released from the water wheel are (9,−3)(9,−3).

Notice at the rotated point in the coordinate plane, the water from a paddle is beginning to be released from the water wheel.

2 / 4

A clock is superimposed on the coordinate plane so its center is at the origin of the coordinate plane, as shown below.

12:40 pm

12:25 pm

11:40 am

Rotating a point that has the coordinates (x,y)(x,y) 180° about the origin in a clockwise or counterclockwise direction, produces a point that has the coordinates (−x,−y)(−x,−y). While the end of the minute-hand of the clock does not lie at the point (7,4)(7,4), the time it represents in minutes does. Substituting the coordinates of this point into our formula to find the rotated point, we get (−7,−4)(−7,−4).

Rotating the minute-hand of the clock in the direction of the rotated point, we can get a reading of what time it is.

Each numerical value on the clock measures 5 minutes for the minute hand and 1 hour for the hour hand. Since the rotated point lies at the number 8 for the clock, the reading of the minute hand is 40 minutes. Since the rotation is clockwise the hour hand is also rotated clockwise to represent a time that is later than 12:10 pm., the correct time after the rotation of the minute-hand is 12:40 pm.

3 / 4

The coordinates of the vertices for triangle ABC that can be graphed in the coordinate plane are A(−8,−6)">A(−8,−6)A(−8,−6), B(−2,−6)">B(−2,−6)B(−2,−6), and C(−5,−3)">C(−5,−3)C(−5,−3). The triangle is rotated 90° in a clockwise direction about the origin to produce triangle A’B’C’. Which of the following are the vertices for triangle A’B’C’?

A′(6,−8) , B′(6,−2) , C′(3,−5)

A′(−6,8) , B′(−6,2) , C′(−3,5)

A′(−8,6) , B′(−6,2) , C′(5,−3)

Rotating a point that has the coordinates (x,y)(x,y) 90° about the origin in a clockwise direction produces a point that has the coordinates (y,−x)(y,−x). Substituting the coordinates for our points into our formula to find the rotated points, we get:

 

A′(−6,−(−8))=A′(−6, 8)A′(−6,−(−8))=A′(−6, 8)
B′(−6,−(−2))=B′(−6, 2)B′(−6,−(−2))=B′(−6, 2)
C′(−3,−(−5))=C′(−3, 5)C′(−3,−(−5))=C′(−3, 5)

Thus, the coordinates for the vertices for triangle A’ B’ C’ are A′(−6,8)A′(−6,8), B′(−6,2)B′(−6,2), and C′(−3,5)C′(−3,5).

4 / 4

On the coordinate plane, point A(3,−4)">A(3,−4)A(3,−4) is rotated 180° in a counterclockwise direction about the origin to create the rotated point A’. Which of the following is the ordered pair for A’?

(4,−3)

(−3,−4)

(−3,4)

(−4,3)

Answer:

Rotating a point that has the coordinates (x,y)(x,y) 180° about the origin in a counterclockwise or clockwise direction produces a point that has the coordinates (−x,−y)(−x,−y). Substituting the coordinates for point A into our formula to find the rotated point, we get:

 

A′(−3,−(−4))=A′(−3, 4)

Your score is

LinkedIn Facebook Twitter VKontakte