How to Find Perimeter of Rectangle
To find the perimeter of a rectangle, use the formula: Perimeter = 2 × (Length + Width). Simply add the length and width, then multiply by 2 to get the perimeter.
What is the perimeter of a rectangle?
The perimeter of a rectangle can be calculated using the formula P = 2 × (L + W), where P is the perimeter, L is the length, and W is the width. By inputting the rectangle’s length and width into this equation, you can easily determine its perimeter. For example, if the rectangle represents a garden that requires a brick border, this formula helps figure out how much brick is needed to go around the garden.
Perimeter of Rectangle Formula
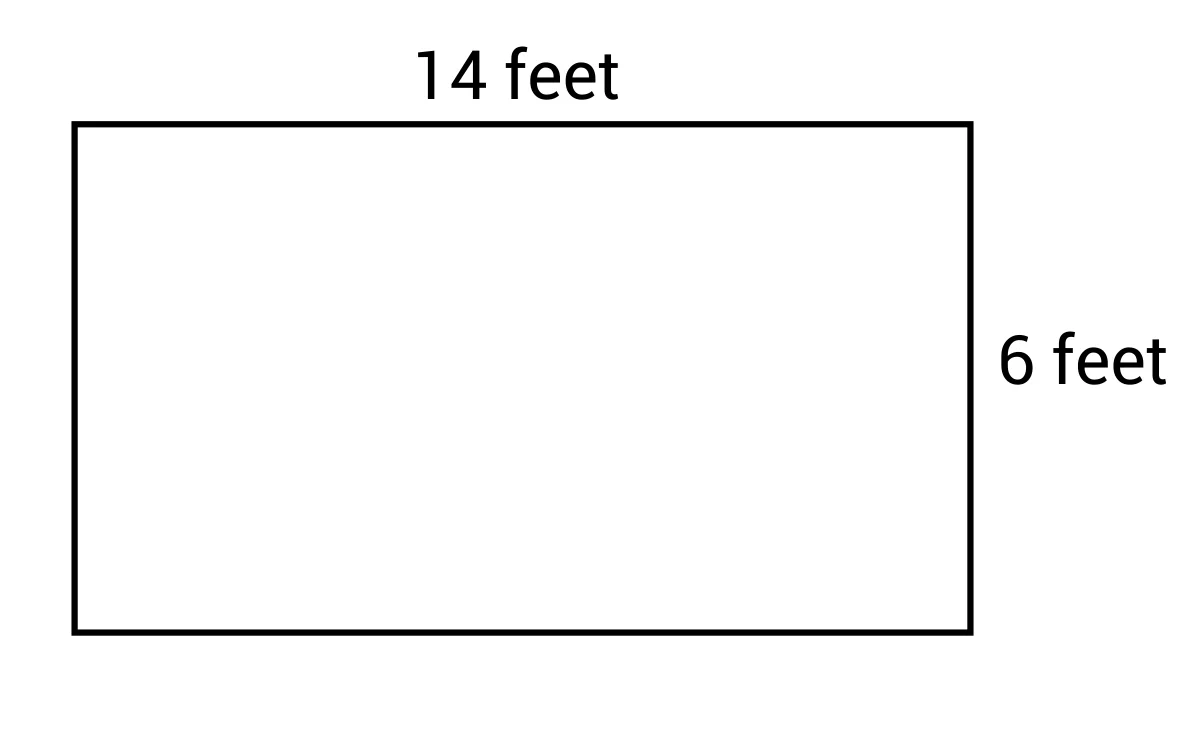
The perimeter formula is P = (L + W) × 2. If we substitute L = 14 feet and W = 6 feet, we get P = (14 + 6) × 2, which simplifies to 40 feet. Using this formula is quicker than adding up the individual sides, like 14 + 6 + 14 + 6, which would also give the correct result but take more time.
However, some perimeter problems don’t give you the length and width directly. Instead, one dimension and the area might be provided. To solve these, remember the formula for area: length × width. For instance, a rectangle measuring 3.5 cm by 4 cm has an area of 14 cm² (3.5 × 4 = 14). Now, let’s use this to tackle a perimeter problem.
For example, if you need to frame a large rectangular window with an area of 35 square feet and a length of 7 feet, we can use the area formula to help us find the perimeter.

Surface area is calculated by multiplying the length by the width. So, for a rectangle with an area of 35, we have 7 × ? = 35. To find the missing side length, divide 35 by 7, which gives 5. Now we can apply the perimeter formula since we know the length is 7 feet and the width is 5 feet.
Using the formula P = (L + W) × 2, we get P = (7 + 5) × 2, which simplifies to 24 feet.
Now, let’s explore the question: Can a rectangle with an area of 20 square feet have more than one possible perimeter?
Yes, it can. A rectangle with an area of 20 square feet can have different perimeter values based on its dimensions. For example, 1 ft × 20 ft, 2 ft × 10 ft, and 4 ft × 5 ft all have the same area but different perimeters. Let’s calculate the perimeter for these rectangles:
1 ft × 20 ft: P = (1 + 20) × 2 = 42 feet
2 ft × 10 ft: P = (2 + 10) × 2 = 24 feet
4 ft × 5 ft: P = (4 + 5) × 2 = 18 feet
Perimeter of a Rectangle Sample Questions

Understanding the Perimeter
The perimeter of a rectangle is the total distance around the outside of the shape. It is a fundamental concept in geometry, often applied in various practical scenarios, such as calculating the length of fencing needed for a garden or the amount of trim required for a room. Knowing how to calculate the perimeter is crucial for both students and professionals in fields involving measurement.
The Formula for a Rectangle’s Perimeter
To compute the perimeter of a rectangle, the formula is straightforward: P = 2(l + w), where “P” represents the perimeter, “l” is the length, and “w” is the width. This equation indicates that you add the lengths of both pairs of opposite sides and then multiply the sum by two. It’s that simple.
Step-by-Step Calculation Example
Let’s consider a rectangle with a length of 8 meters and a width of 3 meters. Following the formula, you would first add the length and width together: 8 + 3 = 11. Then, multiply that sum by 2: 11 x 2 = 22 meters. Therefore, the perimeter of this rectangle is 22 meters.
In summary, learning how to calculate the perimeter of a rectangle not only helps in academic pursuits but also aids in real-life applications. By mastering the formula and understanding the steps involved, you can confidently tackle measurement-related tasks in daily life.
